8551. Последовательности

Вычислите количество неубывающих последовательностей длины n, содержащих целые числа от 1 до m, где каждый элемент встречается не более k раз.

Вход. Три целых числа n, m и k (0 < n, m, k < 31).

Выход. Выведите количество описанных последовательностей.

Пример входа	Пример выхода
3 4 2	16

Последовательностями будут: (1,1,2), (1,1,3), (1,1,4), (1,2,2), (1,2,3), (1,2,4), (1,3,3), (1,3,4), (1,4,4), (2,2,3), (2,2,4), (2,3,3), (2,3,4), (2,4,4), (3,3,4), (3,4,4).

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть f(n, m) равно количеству искомых последовательностей длины n, содержащие числа от 1 до m, где каждый элемент встречается не более k раз.

Число m в последовательности может:

· отсутствовать, тогда следует строить f(n, m – 1) последовательностей;

· стоять в последней позиции. На n – 1 первых позициях строим f(n – 1, m – 1) последовательностей;

· стоять в двух последних позициях. На n – 2 первых позициях строим f(n – 2, m – 1) последовательностей;

· и так далее

· стоять в k последних позициях. На n – k первых позициях строим f(n – k, m – 1) последовательностей;

Базовые случаи:

f(0, m) = 1, в этом случае числа на всех n позициях уже фиксированы.

f(n, 0) = 0, нет возможности построить ни одной последовательности.

f(n, m) = 0 при n < 0.

f(n, m) = 0 при m * k < n. Максимум последовательность может содержать k единиц, k двоек, k троек, …, k m-ок. Если длина последовательности n больше m * k, то такой последовательности не существует.

Пример

Пусть n = 3, m = 4, k = 2. Тогда

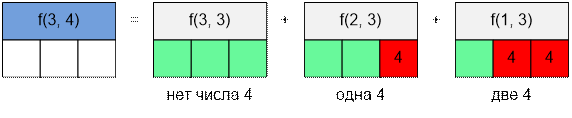
f(3, 3): генерируем последовательности длины 3 из чисел 1, 2, 3.

f(2, 3): генерируем последовательности длины 2 из чисел 1, 2, 3. На третьей позиции стоит 4.

f(1, 3): генерируем последовательности длины 1 из чисел 1, 2, 3. На второй и третьей позиции стоит 4.

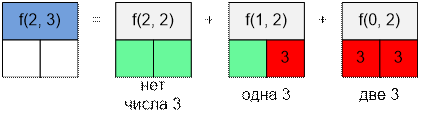
f(2, 3): в двух позициях могут стоять числа 1, 2, 3.

· f(2, 2): в двух позициях могут стоять числа 1, 2. Это последовательности (1, 1), (1, 2), (2, 2). Следовательно f(2, 2) = 3.

· f(1, 2): в одной позиции могут стоять числа 1, 2. Во второй позиции стоит 3. Это последовательности (1, 3), (2, 3). Следовательно f(1, 2) = 2.

· f(0, 2): все позиции заняты. Это последовательность (3, 3). Следовательно f(0, 2) = 1.

f(2, 3) = f(2, 2) + f(1, 2) + f(0, 2) = 3 + 2 + 1 = 6.

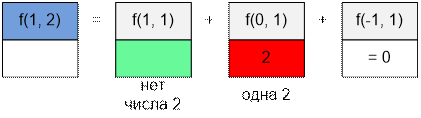
f(1, 2): в одной позиции могут стоять числа 1, 2.

Это последовательности (1) и (2). Следовательно f(1, 2) = 2.

Реализация алгоритма

Объявим массив для запоминания динамики: mas[n][m] = f(n, m).

long long mas[32][32];

Рекурсивная функция вычисления f(n, m).

long long f(int n, int m)

{

if (n == 0) return 1;

if (n < 0 || m == 0) return 0;

if (m * k < n) return 0;

if (mas[n][m] != -1) return mas[n][m];

long long res = 0;

for(int i = 0; i <= k; i++)

res = res + f(n-i,m-1);

return mas[n][m] = res;

}

Основная часть программы. Читаем входные данные и выводим ответ.

scanf("%d %d %d",&n,&m,&k);

memset(mas,-1,sizeof(mas));

printf("%lld\n",f(n,m));